관성모멘트 실험
관성모멘트란 물체가 회전하면서 가지는 운동량과 반대 방향으로 작용하는 모멘트를 의미합니다. 이 모멘트는 물체의 질량과 회전 중심의 위치에 의존하며, 물체의 운동 상태에 따라 변화합니다. 관성모멘트는 회전운동에서 중요한 역할을 수행하는데, 그 이유는 회전할 때 물체를 멈추거나 운동 상태를 변화시키는 데 큰 영향을 미치기 때문입니다.
관성모멘트 공식
관성모멘트는 I(관성모멘트)로 표현되며, 다음과 같은 공식으로 계산됩니다.
I = m X r²
여기에서 m은 물체의 질량, r은 물체의 회전 중심에서의 거리를 나타냅니다. 만약 회전 중심이 물체의 질점과 일치한다면, r은 0이 되어 관성모멘트는 0이 됩니다.
관성모멘트 실험 장비
관성모멘트는 물체가 회전하는 운동에서 발생하는데, 이를 측정하기 위해서는 적절한 장비가 필요합니다. 가장 일반적인 관성모멘트 실험 장비는 회전하는 플랫폼과 이를 회전시키는 모터로 구성되어 있습니다. 플랫폼은 물체를 놓는 플레이트와 회전 중심을 정확하게 맞추는 링으로 구성됩니다. 모터는 플랫폼을 회전시키는 역할을 하며, 회전 속도를 조절할 수 있습니다.
관성모멘트 측정 과정
관성모멘트를 측정하기 위해서는 물체에 힘을 가해 회전운동을 발생시켜야 합니다. 이 때 회전운동은 지속적으로 유지되어야 하며, 물체와 회전 중심이 일치해야 합니다. 이 조건을 충족시켜 관성모멘트를 측정하기 위해서는 다음과 같은 절차를 따릅니다.
1. 물체의 질량을 측정하여 기록합니다.
2. 물체를 플랫폼의 플레이트에 올려놓고, 회전 중심과 일치하도록 조정합니다.
3. 모터를 작동시키고, 회전 속도를 조절하여 안정적인 회전운동이 발생하도록 합니다.
4. 회전 시간을 측정하고, 회전속도를 기록합니다.
5. 회전 중심에서 물체의 질점까지 거리를 측정하여 기록합니다.
6. 관성모멘트 공식을 이용하여 관성모멘트를 계산합니다.
7. 실험 결과를 분석하고, 적절한 통계 분석 방법을 적용하여 결과를 해석합니다.
관성모멘트 연습 문제
아래는 관성모멘트 계산에 대한 연습 문제입니다.
1. 반지름이 0.5m인 플라스틱 원판의 질량은 3kg입니다. 회전 중심에서 원판의 외부까지의 거리는 0.4m입니다. 이 때 원판의 관성모멘트는 얼마입니까?
I = m X r²
I = 3 X 0.4²
I = 1.92 kgm²
2. 반지름이 1.2m인 철재 원판의 질량은 10kg입니다. 회전 중심에서 원판의 외부까지의 거리는 0.8m입니다. 이 때 원판의 관성모멘트는 얼마입니까?
I = m X r²
I = 10 X 0.8²
I = 6.4 kgm²
관성모멘트 활용 사례
관성모멘트는 운동 역학에서 가장 중요한 개념 중 하나입니다. 그 이유는 관성모멘트가 물체의 운동상태를 결정하는 데 큰 영향을 미치기 때문입니다. 예를 들어, 관성모멘트가 큰 자전거의 핸들은 덜 민감하게 반응하며, 관성모멘트가 작은 자전거의 핸들은 민감하게 반응합니다. 이러한 속성은 자전거의 측면으로부터 안정성과 민첩성을 결정합니다.
또한, 관성모멘트는 항공기의 기동성을 결정하는 데도 중요한 역할을 수행합니다. 항공기에는 회전할 때 필요한 관성모멘트를 제공하는 회전바퀴가 설치되어 있습니다. 이 회전바퀴는 항공기의 회전 운동을 안정적으로 지원하며, 기동성을 향상시키는 데 큰 역할을 합니다.
관성모멘트 고급 레벨 연습 문제
아래는 관성모멘트 유도와 질점의 관성모멘트 실험에 대한 고급 레벨 연습 문제입니다.
1. 길이가 1.5m인 고무줄이 끝에 차 있는 고리를 당기면 고무줄이 회전운동을 시작합니다. 이 때 고무줄의 관성모멘트는 어떻게 되나요?
고무줄이 회전운동을 시작할 때, 고무줄의 길이가 늘어나기 때문에 관성모멘트는 점차 커지게 됩니다. 이러한 현상을 관성모멘트 유도라고 합니다.
2. 질점이 달린 지팡이를 회전 장치에 걸어놓고 회전운동을 시작하면, 질점의 관성모멘트를 측정할 수 있습니다. 이 때 질점의 관성모멘트는 어떻게 계산되나요?
질점의 관성모멘트는 다음과 같은 공식으로 계산됩니다.
I = m X r²
여기에서 m은 질점의 질량, r은 질점과 회전 중심 사이의 거리를 나타냅니다.
관성모멘트 실험 실습 결과 분석
관성모멘트 실험 실습의 결과는 다양한 형태로 나타날 수 있습니다. 예를 들어, 회전 장치에 의한 관성모멘트 측정 결과는 회전관성 결과레포트 형태로 제공됩니다. 이 결과는 실험을 위해 우선 회전장치를 구동하는 장비와 측정하는 장비의 세트를 사용한 후 직접적인 측정 결과를 통해 확인할 수 있습니다.
이러한 실험 결과 분석을 통해 관성모멘트 공식이 활용된다는 것을 알 수 있습니다. 예를 들어, 관성모멘트 측정 결과를 통해 제공되는 회전관성 결과레포트를 분석하면, 물체의 질량과 회전 중심 사이의 거리에 따라 관성모멘트가 어떻게 변하는 지를 확인할 수 있습니다. 이를 활용해 다양한 상황에서 관성모멘트를 계산할 수 있으며, 이를 통해 운동 역학 분야에서 유용한 정보를 얻을 수 있습니다.
FAQs
1. 관성모멘트란 무엇인가요?
관성모멘트는 물체가 회전하는 운동에서 가지는 운동량과 반대 방향으로 작용하는 모멘트를 의미합니다. 이는 물체의 질량과 회전 중심의 위치에 의존하며, 물체의 운동 상태에 따라 변화합니다.
2. 관성모멘트는 어떤 역할을 하나요?
관성모멘트는 운동 역학에서 중요한 역할을 수행하는데, 그 이유는 회전할 때 물체를 멈추거나 운동 상태를 변화시키는 데 큰 영향을 미치기 때문입니다.
3. 관성모멘트는 어떻게 측정하나요?
관성모멘트를 측정하기 위해서는 회전하는 플랫폼과 이를 회전시키는 모터로 구성된 측정 장비가 필요합니다. 이를 통해 물체에 힘을 가해 회전운동을 발생시킨 후, 회전시간과 회전 중심에서 물체의 질점까지의 거리를 측정하여 관성모멘트를 계산합니다.
4. 관성모멘트는 어떻게 계산하나요?
관성모멘트는 I(관성모멘트)로 표현되며, 다음과 같은 공식으로 계산됩니다.
I = m X r²
여기에서 m은 물체의 질량, r은 물체의 회전 중심에서의 거리를 나타냅니다.
5. 관성모멘트는 어디에서 활용되나요?
관성모멘트는 운동 역학에서 매우 중요한 개념 중 하나이며, 자동차, 항공기 등 다양한 분야에서 적용됩니다. 예를 들어, 자동차의 조향장치나 항공기의 회전바퀴는 관성모멘트를 활용해 설계됩니다.
사용자가 검색한 키워드: 관성모멘트 실험 관성모멘트 계산, 회전 장치에 의한 관성 모멘트 측정, 회전관성 결과레포트, 관성모멘트 공식, 질량 관성모멘트, 관성모멘트 유도, 질점의 관성모멘트 실험, 관성모멘트 공식 유도
Categories: Top 90 관성모멘트 실험
관성모멘트(회전관성) 실험 (1)
여기에서 자세히 보기: c3.castu.org
관성모멘트 계산
In this article, we will take an in-depth look at how to calculate the moment of inertia and why it’s so important in engineering and physics.
Moments of Inertia of Common Shapes
The moment of inertia is calculated differently for different shapes, and there are specific equations for each shape. Here are a few examples of common shapes and their corresponding equations:
– Rectangular plate: I= (1/12)ML^2
– Circular disk: I= (1/2)MR^2
– Rod rotating about its center: I= (1/12)ML^2
– Thin rod rotating about an endpoint: I= (1/3)ML^2
– Solid cylinder rotating about its center: I= (1/2)MR^2
These equations are based on the mass, dimensions, and axis of rotation of the object.
Calculating the Moment of Inertia
To calculate the moment of inertia of an object, you need to know the mass distribution and the axis of rotation. The moment of inertia is defined as the sum of the products of the mass of each element of the object and the square of its distance from the axis of rotation. This can be expressed mathematically as:
I= Σmr^2
where I is the moment of inertia, Σ is the sum of the individual mass elements, m is the mass of each element, and r is the distance of each element from the axis of rotation.
The moment of inertia can be calculated using calculus integration for objects with continuous mass distribution, such as a rod or a cylinder. For objects with a discrete mass distribution, such as a set of point masses or a system of particles, the moment of inertia can be calculated by summing the product of each mass element and its distance from the axis of rotation.
Applications of Moment of Inertia
Moment of inertia is an important concept in engineering, physics, and mechanics. It is used in designing and optimizing machines, structural beams, and other mechanical systems. Here are some applications of moment of inertia:
– Rotational motion: Moment of inertia is an essential factor in understanding rotational motion. It helps to determine the rotational speed and acceleration of an object around an axis.
– Designing machinery: Moment of inertia plays a crucial role in designing machinery such as flywheels, rotors, and other rotating systems. A proper understanding of moment of inertia helps to optimize the design for the desired performance.
– Structural engineering: Moment of inertia is used in structural engineering to determine the strength of beams and other load-bearing structures. It helps to predict the deformation of a structure under different loads.
FAQs
Q: What is the difference between moment and torque?
A: Torque is the force that causes rotation, while moment refers to the measure of an object’s resistance to rotational motion.
Q: What is the difference between moment of inertia and rotational inertia?
A: Moment of inertia and rotational inertia are the same things.
Q: How do you find the moment of inertia of a composite object, like a cylinder with a hollow section?
A: For a composite object, you can use the parallel-axis theorem to calculate the moment of inertia. The parallel-axis theorem states that the moment of inertia of an object about any axis parallel to its axis of symmetry equals the sum of its moment of inertia about its center of mass and the product of its mass and the square of the distance between the two parallel axes.
Q: Why is moment of inertia important in engineering?
A: Moment of inertia is important in engineering because it helps to predict how objects will behave under different loads and forces. It gives engineers the information they need to design and optimize machines, structural beams, and other mechanical systems.
Q: How is the moment of inertia affected by changing the axis of rotation?
A: Changing the axis of rotation changes the moment of inertia. The moment of inertia is the sum of the products of the mass of each element of the object and the square of its distance from the axis of rotation. As the distance from the axis of rotation changes, so does the moment of inertia.
회전 장치에 의한 관성 모멘트 측정
회전 장치에 의한 관성 모멘트 측정은 일반적으로 기계나 자동차 등의 회전하는 물체에서 발생하는 관성 모멘트를 측정하는 기술이다. 이는 회전하는 물체의 질량 중심이 어디에 있는지를 알아내는 데 매우 중요한 역할을 한다. 회전하는 물체에는 중심축 주변으로 회전하는 관성 모멘트와, 중심축 주변의 회전 중심과 멀어진 축 주변으로 회전하는 관성 모멘트가 있다. 이 두 관성 모멘트는 서로 다른 크기와 방향을 가지고 있으며, 회전하는 물체의 안정성을 결정하는 데 영향을 미치는 중요한 요소이다.
회전 장치를 사용하여 관성 모멘트를 측정하는 방법은 간단하다. 회전 장치에는 회전하는 물체를 고정시킬 수 있는 축과 회전 속도를 계측할 수 있는 센서가 있다. 회전하는 물체를 축에 고정시킨 후 회전 속도를 높여 관성 모멘트를 알아내는 것이다.
회전 장치에 의한 관성 모멘트 측정은 다양한 산업분야에서 활용되고 있다. 예를 들어 자동차 산업에서는 차량의 안정성을 측정하는 데 사용되며, 항공기 산업에서는 비행기 날개와 같은 회전하는 부품의 안정성을 측정하는 데 활용된다. 또한 철도, 해양, 에너지 산업에서도 활용되며, 로봇 공학 분야에서도 많은 활용 가능성을 가지고 있다.
회전하는 물체의 안정성 측정과 관련하여 회전 장치에 사용되는 다양한 센서가 있다. 이 센서들은 회전하는 물체의 속도, 위치, 가속도 등의 정보를 측정할 수 있다. 이 정보들은 회전하는 물체의 안정성 측정뿐만 아니라, 제어 및 모니터링 시스템에 사용될 수 있다.
회전 장치의 종류
회전 장치는 다양한 종류가 있으며, 사용 목적에 따라 선택할 수 있다. 가장 일반적으로 사용되는 회전 장치는 회전하는 물체를 고정시키는 축과 회전 속도를 측정하는 센서로 구성된 부품이다. 그 외에도 다양한 종류가 있으며, 이들 중 일부는 아래와 같다.
– 자동 회전 장치: 회전하는 물체를 자동으로 회전시키는 장치로, 회전 속도를 조절할 수 있다. 이 장치는 테스트 중에 물체를 간단하게 조작할 수 있도록 돕는다.
– 전자식 회전 장치: 전자식 센서를 사용하여 회전 속도를 측정하는 회전 장치이다. 이 장치는 물체에서 발생하는 진동과 관련된 잡음을 줄여준다.
– 하이테크 회전 장치: 다양한 기능과 모니터링을 수행하는 고급 회전 장치이다. 이 장치는 정밀하고 안정적인 측정을 위해 다양한 센서를 사용한다.
– 휴대용 회전 장치: 이 장치는 소형이며, 이동성이 뛰어나다. 휴대용 회전 장치는 공간이 제한된 장소에서 회전하는 물체를 측정하는 데 사용된다.
FAQ
1. 회전 장치에 대한 중요성은 무엇인가요?
– 회전 장치는 회전하는 물체의 안정성을 측정하는 데 매우 중요하다. 이를 통해 안정성에 대한 정보를 제공하여 물체에서 발생할 수 있는 위험을 예방할 수 있다.
2. 회전 장치는 어디에 사용되나요?
– 회전 장치는 다양한 산업분야에서 사용된다. 자동차 산업에서는 차량의 안정성을 측정하는 데 사용되며, 항공기 산업에서는 회전하는 부품의 안정성을 측정하는 데 사용된다. 또한 철도, 해양, 에너지 산업에서도 활용되며, 로봇 공학 분야에서도 많은 활용 가능성을 가지고 있다.
3. 회전 장치의 센서는 어떤 정보를 제공하나요?
– 회전 장치의 센서는 회전하는 물체의 속도, 위치, 가속도 등의 정보를 제공한다. 이 정보들은 회전하는 물체의 안정성 측정뿐만 아니라, 제어 및 모니터링 시스템에 사용될 수 있다.
4. 회전 장치의 종류는 어떤 것이 있나요?
– 회전 장치의 종류에는 자동 회전 장치, 전자식 회전 장치, 하이테크 회전 장치, 휴대용 회전 장치 등이 있다. 이들 중 사용 목적에 따라 선택할 수 있다.
5. 회전 장치를 사용하는 것은 어렵나요?
– 회전 장치를 사용하는 것은 비교적 간단하다. 단지 회전하는 물체를 축에 고정시킨 후 회전 속도를 높이면 관성 모멘트를 측정할 수 있다. 그러나 전문적인 장비를 사용할 경우 훨씬 정밀한 측정이 가능하다.
6. 회전하는 물체의 안정성을 확인하는 데 회전 장치를 사용하는 것이 왜 중요한가요?
– 회전하는 물체의 안정성을 확인하는 것은 매우 중요하다. 안정성이 부족한 물체에서는 사실상 폭발적인 결과를 초래할 수 있다. 회전 장치를 사용하여 안정성을 확인할 수 있으므로 이를 예방할 수 있다.
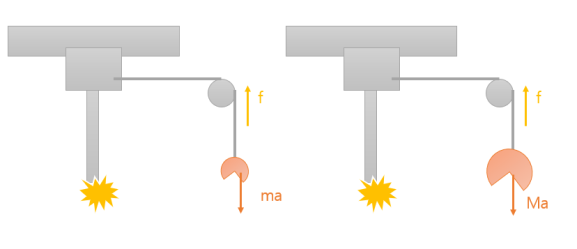
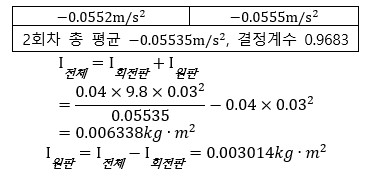
주제와 관련된 이미지 관성모멘트 실험

관성모멘트 실험 주제와 관련된 이미지 30개를 찾았습니다.


.gif)



.gif)

.gif)




.gif)


.gif)


.gif)

Article link: 관성모멘트 실험.
주제에 대해 자세히 알아보기 관성모멘트 실험.
- 관성 모멘트 측정 실험 – 네이버 블로그
- 관성 모멘트 측정 – 서울시립대학교
- 【물리학 실험】 3강. 관성모멘트 실험 – 정빈이의 공부방
- 물리학실험1 관성 모멘트 측정 – Gyojun Youn’s PS Blog
- 관성모멘트 – 연세대학교 물리학실험실(Yonsei Phylab)
- 대학물리실험 – 관성 모멘트
- 관성모멘트 족보 – 관성모멘트 레포트입니다. 참고하시면 좋을 …
더보기: blog https://c3.castu.org/danh-muc/lam-dep